dérivable

dérivable

dérivable [ derivabl ] adj.
• 1904; de 1. dériver
♦ Qui peut être dérivé. — Math. Fonction dérivable en un point, qui admet une dérivée en ce point. Fonction dérivable sur un intervalle de son domaine de définition.

● dérivable adjectif Se dit d'une fonction qui a une dérivée. (On distingue, selon les cas, les fonctions dérivables à droite ou à gauche, dérivables sur un intervalle ouvert ou fermé, dérivables n fois ou indéfiniment dérivables.)

dérivable
adj. MATH Fonction dérivable en un point, qui admet une dérivée en ce point.

⇒DÉRIVABLE, adj.
Qui peut être dérivé.
A.— BALIST. Dont le plan de tir peut être dévié du côté opposé à la dérivation (cf. dériver1 B rem. 1) :
• Les carabines actuelles permettent une adaptation à la morphologie de chaque individu, les appareils de visée dérivables en hauteur et en largeur offrent la possibilité d'un réglage très précis de l'arme...
Jeux et sp., 1968, p. 1455.
B.— MATH. [En parlant d'une fonction] Dont on peut trouver la dérivée en un point ou dans un intervalle. Fonction dérivable. Cf. Gds cour. pensée math., 1948, p. 181.
Prononc. :[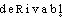]. Étymol. et Hist. 1904 [fonctions] dérivables (LEBESGUE, Intégr. et rech. fonctions primit., p. 72). Dér. du rad. de dériver1; suff. -able. Fréq. abs. littér. :1.
DÉR. Dérivabilité, subst. fém. Propriété pour une fonction d'être dérivable. Cf. Hist. gén. sc., t. 3, vol. 2, 1964, p. 57. — [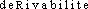]. — 1re attest. 1961 (Hist. gén. sc., t. 3, vol. 1, p. 63); de dérivable, suff. -ité.

dérivable [deʀivabl] adj.
ÉTYM. 1904; de 1. dériver, et -able.
❖
♦ Qui peut être dérivé. — Math. || Fonction dérivable en un point, qui admet une dérivée en ce point. || Fonction dérivable sur un intervalle de son domaine de définition.

Encyclopédie Universelle. 2012.

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Derivable — De*riv a*ble, a. [From {Derive}.] That can be derived; obtainable by transmission; capable of being known by inference, as from premises or data; capable of being traced, as from a radical; as, income is derivable from various sources. [1913… …   The Collaborative International Dictionary of English

  • derivable — index deductible (provable) Burton s Legal Thesaurus. William C. Burton. 2006 …   Law dictionary

  • derivable — [adj] deducible a priori, attributable, available, determinable, dogmatic, extractable, inferable, likely, obtainable, reasoned, resultant, traceable; concept 529 Ant. inconcludable, underivable …   New thesaurus

  • Dérivable — Dérivée  Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… …   Wikipédia en Français

  • derivable — adjective able to be derived, deducible Ant: underivable, non derivable See Also: derivability …   Wiktionary

  • dérivable — (dé ri va bl ) adj. Qu on peut dériver. Ce principe est dérivable de tel autre. ÉTYMOLOGIE    Dériver 2 …   Dictionnaire de la Langue Française d'Émile Littré

  • derivable — de|riv|a|ble [dıˈraıvəbəl] adj [+from] something that is derivable can be calculated from something else …   Dictionary of contemporary English

  • derivable — adjective formal something that is derivable can be calculated from something else …   Longman dictionary of contemporary English

  • derivable — derive ► VERB (derive from) 1) obtain (something) from (a source). 2) base (something) on a modification of. 3) have as a root or origin; originate from. DERIVATIVES derivable adjective. ORIGIN originally meaning «draw a fluid through or into a… …   English terms dictionary

  • derivable — adjective Date: 1653 capable of being derived …   New Collegiate Dictionary

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”